Set operations

This family of functions treats ivs as sets. They always compute the minimal iv of each input and return a minimal iv.

• iv_set_complement() takes the complement of the intervals in an iv. By default, the minimum and maximum of the inputs define the bounds to take the complement over, but this can be adjusted with lower and upper. Missing intervals are always dropped in the complement.

• iv_set_union() answers the question, "Which intervals are in x or y?" It is equivalent to combining the two vectors together and then calling iv_groups().

• iv_set_intersect() answers the question, "Which intervals are in x and y?"

• iv_set_difference() answers the question, "Which intervals are in x but not y?" Note that this is an asymmetrical difference.

• iv_set_symmetric_difference() answers the question, "Which intervals are in x or y but not both?"

Usage

iv_set_complement(x, ..., lower = NULL, upper = NULL)

iv_set_union(x, y)

iv_set_intersect(x, y)

iv_set_difference(x, y)

iv_set_symmetric_difference(x, y)

Arguments

x

[iv]

An interval vector.

...

These dots are for future extensions and must be empty.

lower, upper

[vector(1) / NULL]

Bounds for the universe over which to compute the complement. These should have the same type as the element type of the interval vector. It is often useful to expand the universe to, say, -Inf to Inf.

y

[iv]

An interval vector.

Value

• For iv_set_complement(), a vector of the same type as x containing the complement.

• For all other set operations, a vector of the same type as the common type of x and y containing the result.

Graphical Representation

Graphically, generating the complement looks like:

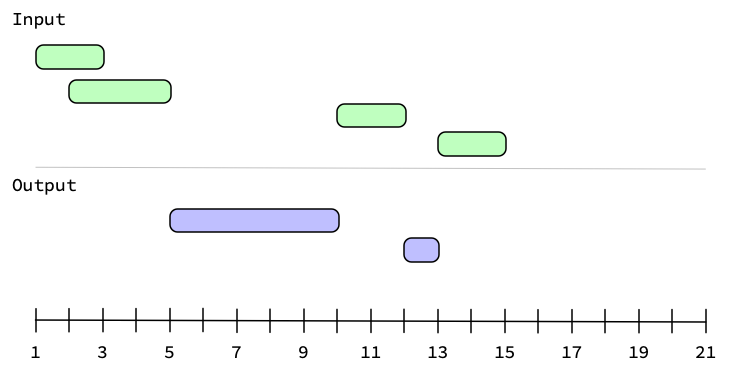
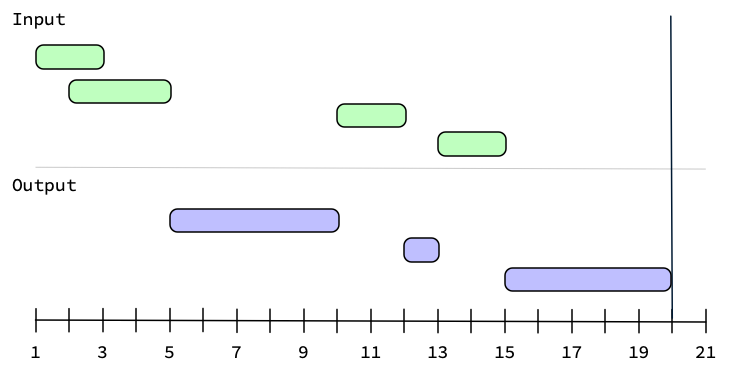
If you were to set upper = 20 with these intervals, then you'd get one more interval in the complement.

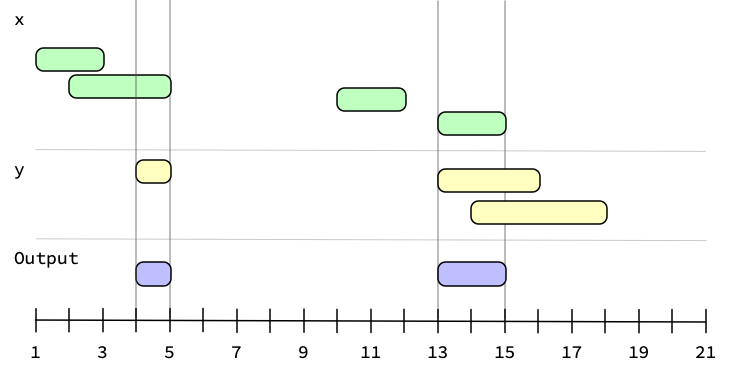
Generating the intersection between two ivs looks like:

See also

The pairwise versions of these functions, such as iv_pairwise_set_union().

Examples

x <- iv_pairs(
  c(10, 12),
  c(0, 5),
  c(NA, NA),
  c(3, 6),
  c(-5, -2),
  c(NA, NA)
)
x
#> <iv<double>[6]>
#> [1] [10, 12) [0, 5)   [NA, NA) [3, 6)   [-5, -2) [NA, NA)

y <- iv_pairs(
  c(2, 7),
  c(NA, NA),
  c(-3, -1),
  c(14, 15)
)
y
#> <iv<double>[4]>
#> [1] [2, 7)   [NA, NA) [-3, -1) [14, 15)

# Complement contains any values from `[-5, 12)` that aren't represented
# in these intervals. Missing intervals are dropped.
iv_set_complement(x)
#> <iv<double>[2]>
#> [1] [-2, 0) [6, 10)

# Expand out the "universe" of possible values
iv_set_complement(x, lower = -Inf)
#> <iv<double>[3]>
#> [1] [-Inf, -5) [-2, 0)    [6, 10)   
iv_set_complement(x, lower = -Inf, upper = Inf)
#> <iv<double>[4]>
#> [1] [-Inf, -5) [-2, 0)    [6, 10)    [12, Inf) 

# Which intervals are in x or y?
iv_set_union(x, y)
#> <iv<double>[5]>
#> [1] [-5, -1) [0, 7)   [10, 12) [14, 15) [NA, NA)

# Which intervals are in x and y?
iv_set_intersect(x, y)
#> <iv<double>[3]>
#> [1] [-3, -2) [2, 6)   [NA, NA)

# Which intervals are in x but not y?
iv_set_difference(x, y)
#> <iv<double>[3]>
#> [1] [-5, -3) [0, 2)   [10, 12)

# Which intervals are in y but not x?
iv_set_difference(y, x)
#> <iv<double>[3]>
#> [1] [-2, -1) [6, 7)   [14, 15)

# Missing intervals in x are kept if there aren't missing intervals in y
iv_set_difference(x, iv(1, 2))
#> <iv<double>[5]>
#> [1] [-5, -2) [0, 1)   [2, 6)   [10, 12) [NA, NA)

# Which intervals are in x or y but not both?
iv_set_symmetric_difference(x, y)
#> <iv<double>[6]>
#> [1] [-5, -3) [-2, -1) [0, 2)   [6, 7)   [10, 12) [14, 15)

# Missing intervals will be kept if they only appear on one side
iv_set_symmetric_difference(x, iv(1, 2))
#> <iv<double>[5]>
#> [1] [-5, -2) [0, 1)   [2, 6)   [10, 12) [NA, NA)
iv_set_symmetric_difference(iv(1, 2), x)
#> <iv<double>[5]>
#> [1] [-5, -2) [0, 1)   [2, 6)   [10, 12) [NA, NA)